Class reference¶
Parameters¶
- class myFitter.Parameter(value=None, default=0.0, scale=1.0, bounds=(None, None), generator=None, rng=<module 'random' from '/usr/lib/python2.7/random.pyc'>)¶
Class describing a fit parameter.
Parameters: - value (float or None, optional) – Value of the parameter. Set to None if the parameter is free to float in the fit. Defaults to None.
- default (float, optional) – Some sensible default value for the parameter. Set to zero if not specified.
- scale (float, optional) – The typical size of variations in this parameter. Defaults to 1.
- bounds (tuple, optional) – Tuple containing the lower and upper bounds (in that order) on the parameter. Use None as first or second element to leave the parameter unbounded from below or above, respectively. Defaults to (None, None).
- generator (callable, optional) – Function which generates random values for the parameter. The supplied function should take no arguments. If omitted or set to None, a sensible default is chosen based on the upper and lower bounds. For an unbounded parameter a normal distribution with mean default and a standard deviation scale is chosen. If only one bound is present, a log-normal distribution is chosen for the distance from that bound. The distribution is centered on default and has a width of scale. If a lower and upper bound are present, the distribution is uniform between those bounds.
- rng (object or module, optional) – The random number generator to use. This is only relevant if generator was not specified or set to None. Set it to an instance of random.Random or the random module itself. The latter is the default.
- value¶
float or None
Value of the parameter. Set to None if the parameter is free to float in the fit. Defaults to None.
- default¶
float
Default value of the parameter.
- scale¶
float
The typical size of variations in this parameter. Defaults to 1.
- lowerBound¶
float or None
Lower bound on the parameter. Set this to None to make the parameter unbounded from below. Defaults to None.
- upperBound¶
float or None
Upper bound on the parameter. Set this to None to make the parameter unbounded from above. Defaults to None.
- generate¶
callable
Function which generates random values for the parameter. It takes no arguments. This is either the function supplied through the generator keyword or the default setting, if no generator keyword was supplied.
- setBounds(l, u)¶
Sets the lower and upper bounds of the parameter.
Parameters: - l (float or None) – Lower bound. Use None to leave parameter unbounded from below.
- u (float or None) – Upper bound. Use None to leave parameter unbounded from above.
Constraints¶
- class myFitter.Constraint(f, rel, bound, scale=1.0, active=True)¶
Class describing constraints on a model’s parameter space.
Parameters: - f (str or callable) – The constraint function. The function will be applied to the dictionary returned by the getDependentQuantities() method of the constrained model. If f is a string, the quantity with that name is used as constraint function.
- rel (‘<’, ‘>’ or ‘=’) – The constraint relation.
- bound (float) – The bound (right-hand side) of the constraint.
- scale (float, optional) – Typical size of variations in the constraint function f.
- active (bool, optional) – If set to False the constraint is ignored. Defaults to True.
- __call__(q)¶
Compute the constraint function.
Parameters: q (dict) – Dictionary with all dependent quantities of the model to be constrained. This will be the dict returned by the getDependentQuantities method of the model under consideration. Returns: The value c of the constraint. If the equality attribute is False, the constraint is satisfied if c >= 0. If the equaltiy attribute is True, constraint is satisfied if c == 0. Return type: float
Chi-square contributions¶
- class myFitter.ChiSquareContribution(active=True)¶
Abstract class describing contributions to the chi-square function.
Parameters: active (bool, optional) – If set to False the contribution is - active¶
bool
If set to False the contribution is ignored. Defaults
- to ``True``.
- __call__(q, x)¶
Compute the chi-square contribution.
Note
Derived classes must implement this. The relation between the likelihood function f and the chi-square function chisq (represented by this method) is:
f(q, x) = exp(-chisq(q,x)/2)
The integral of f over x for fixed q must be 1. Derived classes must ensure that this is the case.
Parameters: - q (dict) – Dictionary containing the model parameters and dependent quantities, as returned by the model’s getDependentQuantites method.
- x (dict) – Dictionary containing the (observed) values of the observables
Returns: The value of the chi-square function for the specified parameters q and observables x.
Return type: float
- getCentralValues(q)¶
Obtain Minimum of the chi-square contribution in observable space.
Note
Derived classes must implement this.
Parameters: q (dict) – Dictionary holding the model parameters and dependent quantites (as returned by getDependentQuantites). Returns: A dictionary describing the position of the minimum of the chi-square contribution in observable space for fixed parameters q. Valid keys of x0 are the names of the observables constrained by this contribution, as returned by the getObservableNames method.
- getObservableNames()¶
Obtain the observables which the chi-square contribution constrains.
Note
Derived classes must implement this.
- getQuadraticForm(q)¶
Obtain the quadratic form on observable space.
Note
Derived classes must implement this.
Parameters: q (dict) – Dictionary holding the model parameters and dependent quantites (as returned by getDependentQuantites). Returns: A dictionary whose entries are of the form (i,j) : Qij, where i and j are names of observables which are constrained by this contribution (i.e. elements of the list returned by the getObservableNames method). Qij is the corresponding entry in the observable space matrix. Only non-zero entries must be included in the dictionary. The matrix should be symmetric. For each pair (i,j) with i != j the pair (j,i) should also be a valid key and the associated value should also be Qij.
- min(x)¶
Return the smallest possible chi-square value.
Parameters: x (dict) – Dictionary containing the (observed) values of the observables
- class myFitter.GaussianCSC(obs, err, syst=None, mean=None, active=True)¶
Describes a gaussian contribution with fixed standard deviation.
Parameters: - obs (str) – Name of the constrained observable.
- err (float) – The standard deviation of the gaussian.
- syst (str or None, optional) – Name of the nuisance parameter associated with the systematic error. The mean of the gaussian is defined by the sum of the quantities mean and syst. Defaults to None, which means that there is no systematic error.
- mean (str, optional) – Name of the mean value of obs, as it appears in the dictionary returned by the model’s getDependentQuantities method. Defaults to None, which means that mean is the same as obs.
- active (bool, optional) – If set to False the contribution is ignored. Defaults to True.
- obs¶
str
Name of the constrained observable.
- err¶
float
The standard deviation of the gaussian.
- syst¶
str or None
The name of the nuisance parameter describing the systematic error. Defaults to None, which means that there is no systematic error.
- mean¶
str
Name of the mean value of obs, as it appears in the dictionary returned by the model’s getDependentQuantities method. Defaults to obs.
Describes the contribution of several correlated gaussian observables.
Parameters: - sigma (dict) – Dictionary containing the standard deviations of all contributing observables.
- cor (dict) – Dictionary containing the entries of the correlation matrix. The keys in cor must be tuples (o1, o2), where o1 and o2 must be valid keys of sigma. If (o1, o2) appears in cor, (o2, o1) must not appear. For pairs not appearing in cor, a correlation coefficient of 0 is assumed.
- means (dict, optional) – Dictionary containing the names of the mean values for the constrained observables. means must contain key-value pairs o:m, where o is a valid key in sigma and m is a valid key in the dictionary returned by the model’s getDependentQuantities method.
- active (bool, optional) – If set to False the contribution is ignored. Defaults to True.
Raises: ValueError – If the correlations specified in cor are invalid.
Models¶
- class myFitter.Model¶
Base class for describing a model.
- par¶
dict
Specifies the independent parameters of the model. The keys must be strings. The values must be Parameter instances.
- obs¶
dict
Specifies the ‘measured’ values of the observables. The keys must be strings. The values must be floats.
- con¶
dict
Contains the constraints imposed on the model’s parameter space. The keys must be strings. The values must be instances of Constraint.
- csc¶
dict
Contains the contributions of the chi-square function. The keys must be strings. The values must be instances of ChiSquareContribution.
- nuisanceCSCs¶
set of str
Names of the CSCs which are associated to nuisance parameters.
- activateAllCSCs(ignorenp=True)¶
Activate all chi-square contributions.
Parameters: ignorenp (bool, optional) – If True, settings for chi-square contributions from nuisance parameters are not altered. Defaults to True.
- activateAllConstraints()¶
Activate all constraints.
- activateCSCs(*args)¶
Activate given set of chi-square contributions.
Parameters: *args (str) – Names of the chi-square contributions to activate.
- activateConstraints(*args)¶
Activate given set of constraints.
- activateOnlyCSCs(*args, **kwargs)¶
Activate given set of chi-square contributions, deactivate all others.
Parameters: - *args (str) – Names of the chi-square contributions to activate.
- ignorenp (bool, optional) – If True, settings for chi-square contributions from nuisance parameters are not altered. Defaults to True.
- activateOnlyConstraints(*args)¶
Activate given set of constraints, deactivate all others.
- addConstraint(f, rel, bound, scale=1.0, active=True, name=None)¶
Add a constraint on a model’s parameter space.
Parameters: - f (str or callable) – The constraint function. The function will be applied to the dictionary returned by the getDependentQuantities() method of the constrained model. If f is a string, the dependent quantity with that name is used as constraint function.
- rel ('<', '>', '=' or 'in') – The constraint relation. With 'in' you can constraint f to lie in a finite range. In this case two constraints (one for the lower and one for the upper bound) are added to the con dictionary.
- bound (float) – The bound (right-hand side) of the constraint. If rel is 'in' this must be a tuple holding the lower and upper bound.
- scale (float, optional) – Typical size of variations in the constraint function f.
- active (bool, optional) – If set to False the constraint is ignored. Defaults to True.
- name (str, optional) – The name of the constraint (i.e. the key under which it is added to the con dictionary). If f is a callable this must be specified. If f is a string and name is not specified a name is generated by appending rel to f. If rel is 'in' the value of name can be a tuple of two strings (the name for the lower bound and the name for the upper bound) or a string (in which case names for the lower and upper bounds are generated by appending '<' and '>' to name).
Add a correlated Gaussian contribution to the chi-square function.
Parameters: - name (str) – Name identifying the contribution. A CorrelatedGaussianCSC instance is added to the csc dict under this key.
- obs (iterable) – Contains tuples of the form (obsname, val, err) where obsname is the name of an observable, val is the measured value and err the standard deviation. obsname should be a valid key in the dictionary returned by getDependentQuantities. The associated value defines the mean of the gaussian distribution. The value val is added to the obs dict under the key obsname.
- cor (iterable) – Contains tuple of the form (obs1, obs2, r) where obs1 and obs2 are observable names previously mentioned in the obs argument and r is the associated correlation coefficient.
Raises: NameError – Raised when name is already used in the csc dict or any of the observable names in the obs argument are mentioned twice or already exist as keys in the obs attribute. It is also raised when a correlation coefficient is mentioned twice in the cor argument.
Add a correlated Gaussian nuisance parameters to the model.
This adds several properly initialised Parameter instances to the par dict and a properly initialised CorrelatedGaussianCST instance to the csc dict.
Parameters: - name (str) – Name identifying the set of nuisance parameters. The CorrelatedGaussianCSC instance is added to the csc dict under this key.
- par (iterable) – Contains tuples of the form (parname, val, err) where parname is the name of a (new) nuisance parameter, val is the mean value of that parameter err the standard deviation in the chi-square contribution. val will also be used as the parameters default value and err as its scale.
- cor (iterable) – Contains tuple of the form (par1, par2, r) where par1 and par2 are parameter names previously mentioned in the par argument and r is the associated correlation coefficient.
- addGaussianCSC(name, val, err, syst=None, **kwargs)¶
Add a gaussian contribution to the chi-square function.
Parameters: - name (str) – Name of the observable. It should be a valid key in the dictionary returned by getDependentQuantities. The associated value defines the mean of the gaussian distribution. name is also the key under which an instance of GaussianCSC is added to the csc dict.
- val (float) – Measured value of the observable. This value is added to the obs dict under the key name.
- err (float) – The standard deviation of the gaussian.
- syst – Systematic error(s). If the value is not None a nuisance parameter is added to the model. The name of this parameter is composed by appending ‘ syst’ to name and its range is from -syst to +syst if syst is a float or from -syst[1] to +syst[0] if syst is a tuple. The mean of the gaussian is then defined by the sum of the quantity name and the nuisance parameter. Defaults to None, which means that there is no systematic error.
Raises: NameError – Raised when name is already used in the csc or obs dicts.
- addGaussianNP(name, val, err, syst=None)¶
Add a nuisance parameter with a gaussian error to the model.
This adds a properly initialised Parameter instance to the par dict and a properly initialised GaussianCSC instance to the csc dict.
Parameters: - name (str) – Name of the nuisance parameter. This is the key under which the parameter is added to the par dict and also the key under which the GaussianCSC instance is added to the csc dict.
- val (float) – Central value of the parameter. This value serves as default value for the parameter and as mean value for the gaussian chi-square contribution.
- err (float) – The standard deviation of the gaussian. This value serves as scale for the parameter and as standard deviation for the gaussian chi-square contribution.
- syst (None or float or tuple of floats, optional) – Systematic error. See documentation of addGaussianCSC.
- addParameter(name, **kwargs)¶
Add a parameter to the model.
Parameters: name – Unique string which identifies the parameter.
- addSystematicNP(name, val, syst)¶
Add a nuisance parameter with a systematic error to the model.
Parameters: - name (str) – Name of the nuisance parameter. This is the key under which the parameter is added to the par dict.
- val (float) – Central value of the parameter. This value serves as default value for the parameter.
- syst (float or tuple of floats) – Systematic error. If a float is given, a symmetric systematic error is assumed. For a tuple, the first element is the ‘plus’ error and the second element the ‘minus’ error. Both numbers should be positive.
- chisq(p, obs=None, only=None, exclude=[])¶
Compute the chi-square value for given parameters and observables.
Parameters: - p (dict) – Contains the values of the free parameters
- obs (dict, optional) – Contains the values of the observables. Uses self.obs if omitted.
- only (list or None, optional) – Only include the listed chi-square contributions. Defaults to None, in which case all active chi-square contributions are included. Inactive contributions are never included.
- exclude (list, optional) – Exclude listed chi-square contributions from sum. Defaults to [].
Returns: The chi-square value for parameters p and observables obs.
Return type: float
- copy()¶
Return a deep copy of the model.
- dchisq(p, obs=None, only=None, exclude=[])¶
Compute the Delta chi-square value for given parameters and observables.
Parameters: - p (dict) – Contains the values of the free parameters
- obs (dict, optional) – Contains the values of the observables. Uses self.obs if omitted.
- only (list or None, optional) – Only include the listed chi-square contributions. Defaults to None, in which case all active chi-square contributions are included. Inactive contributions are never included.
- exclude (list, optional) – Exclude listed chi-square contributions from sum. Defaults to [].
Returns: The chi-square value for parameters p and observables obs.
Return type: float
- deactivateAllCSCs(ignorenp=True)¶
Deactivate all chi-square contributions.
Parameters: ignorenp (bool, optional) – If True, settings for chi-square contributions from nuisance parameters are not altered. Defaults to True.
- deactivateAllConstraints()¶
Deactivate all constraints.
- deactivateCSCs(*args)¶
Deactivate given set of chi-square contributions.
Parameters: *args (str) – Names of the chi-square contributions to deactivate.
- deactivateConstraints(*args)¶
Activate given set of chi-square contributions.
- deactivateOnlyCSCs(*args, **kwargs)¶
Deactivate given set of chi-square contributions, activate all others.
Parameters: - *args (str) – Names of the chi-square contributions to deactivate.
- ignorenp (bool, optional) – If True, settings for chi-square contributions from nuisance parameters are not altered. Defaults to True.
- deactivateOnlyConstraints(*args)¶
Deactivate given set of constraints, activate all others.
- fix(*args)¶
Fix model parameters.
Parameters: *args (str or list of str or dict) – Parameters to fix. For string arguments or lists of strings the corresponding parameter(s) are fixed to their default values.
- generateParameterPoint()¶
Generate a random point in parameter space.
Returns: A dictionary of the randomly generated parameters. Fixed parameters are included in the dictionary and will have their fixed values.
- getCentralValues(q)¶
Obtain Minimum of the chi-square function in observable space.
Parameters: q (dict) – Dictionary holding the model parameters and dependent quantites (as returned by getDependentQuantites). Returns: A dictionary describing the position of the minimum of the chi-square function in observable space for fixed parameters q. Valid keys are the names of the observables constrained by the chi-square function, as returned by the getObservableNames method.
- getChiSquare(q, obs=None)¶
Compute the chi-square value from dependent quantities.
This function computes the chi-square value by calling the getChiSquare methods of all active ChiSquareContribution objects in the csc member and adding up the results.
Parameters: - q (dict) – Contains the parameters and dependent quantities, as returned by the getDependentQuantities method.
- obs (dict, optional) – Contains the measured values of the observables. The keys must be those returned by getObservableNames. The values must be floats. If omitted, the content of the obs member is used.
Returns: The value of the chi-square function.
Return type: float
- getConstraintViolation(q)¶
Compute the amount of constraint violation.
Note
This function returns the sum of the squares of the constraint functions for all violated constraints
Parameters: q (dict) – Contains the parameters and dependent quantities, as returned by the getDependentQuantities method.
- getConstraints(q)¶
Compute the constraint functions.
Parameters: q (dict) – Contains the parameters and dependent quantities, as returned by the getDependentQuantities method. Returns: A dictionary containing the values of the active constraint functions. The keys are a subset of those found in the con member. The values are floats.
- getDefaultParameters()¶
Obtain a dictionary with the default values of all model parameters.
- getDeltaChiSquare(q, obs=None)¶
Compute the Delta chi-square value from dependent quantities.
This function computes the chi-square value minus the absolute lower bound on the chi-square value by calling the getChiSquare and min methods of all active ChiSquareContribution objects in the csc member and adding up the results.
Parameters: - q (dict) – Contains the parameters and dependent quantities, as returned by the getDependentQuantities method.
- obs (dict, optional) – Contains the measured values of the observables. The keys must be those returned by getObservableNames. The values must be floats. If omitted, the content of the obs member is used.
Returns: The value of the chi-square function.
Return type: float
- getDependentQuantities(p)¶
Compute all quantities depending on the model parameters.
Parameters: p (dict) – Contains the values of the model parameters. The keys must be the same as those of the par member. The values must be floats. Returns: A dictionary containing the parameters from p and all quantities which depend on them. The keys are strings and the values are floats. Note
The default implementation returns a dictionary with the full set of model parameters, using default values for parameters not specified in p and overriding the values of fixed parameters. Derived classes should add all dependent quantities to the dictionary. Instances of ChiSquareContribution and Constraint will use the dictionary returned by this method to compute the chi-square contributions and the values of the constraint functions, so all quantities needed for these computations should be included. For instances of GaussianCSC this means including the mean value of the corresponding observable. You may use the same string identifier for the observable and the mean.
- getFixedParameters()¶
Obtain a dictionary of the fixed parameters and their values.
Returns: A dictionary containing the names and values of the parameters which are fixed.
- getFreeParameters()¶
Obtain the names of the parameters floating in the fit.
Returns: A list of strings containing the names of the parameters which are free to float in the fit (possibly with lower or upper bounds).
- getObservableNames()¶
Obtain the names of the observables predicted by the model.
Returns: A list of strings containing the names of the observables predicted by the model. Note
This list is compiled by calling the getObservableNames method of all elements of the csc attribute and has nothing to do with the keys found in the obs attribute.
- getQuadraticForm(q)¶
Obtain the quadratic form on observable space.
Note
The quadratic form is obtained by calling the getQuadraticForm method of all active chi-square contributions and adding up the results.
Parameters: q (dict) – Dictionary holding the model parameters and dependent quantites (as returned by getDependentQuantites). Returns: A dictionary whose entries are are of the form (i,j) : Qij, where i and j are names of observables which are constrained by the chi-square function (i.e. elements of the list returned by the getObservableNames method). Qij is the corresponding entry in the observable space matrix. Zero entries may be omitted in the dictionary. The matrix is symmetric.
- release(*args)¶
Release model parameters (allowing them to float in a fit).
Parameters: *args (str or list of str) – Names of the parameters to release
Fits¶
- class myFitter.FitResult(bestFitParameters=None, minChiSquare=None, status=None, success=None, feasible=None, message=None, nEvaluations=None, constraintViolation=None)¶
Stores the results of a localFit call.
Note
For each keyword argument there is an attribute with the same name. All keyword arguments default to None.
Parameters: - bestFitParameters (dict, optional) – Holds the parameter values at the best-fit point.
- minChiSquare (float, optional) – The chi-square value at the minimum.
- success (bool, optional) – True if the minimization terminated successfully.
- feasible (bool, optional) – True if the solution has an acceptably small constraint violation.
- status (int, optional) – Exit code returned by the minimizer.
- message (str, optional) – Message returned by the minimizer.
- nEvaluations (int, optional) – Number of function evaluations.
- constraintViolation (float, optional) – Sum of the squares of the constraint functions which violate constraints.
- __ge__(other)¶
x.__ge__(y) <==> x>=y
- __gt__(other)¶
x.__gt__(y) <==> x>y
- __le__(other)¶
x.__le__(y) <==> x<=y
- copy()¶
Return a deep copy.
- class myFitter.Fitter(model, tries=1, retries=0, cvmargin=10.0, maxcv=0.0001, solver='slsqp', solvercfg={}, par={}, obs=None, neighbours=2, temperature=1.0, penalty=1.0)¶
Sample a model’s parameter space and minimise the chi-square.
Parameters: - model (Model instance) – The model to fit.
- tries (int, optional) – The number of local minimizations to try. Defaults to 1.
- retries (int, optional) – Maximum number of retries (with a different starting point) after a failed minimization. Defaults to 0.
- cvmargin (float, optional) – The acceptable amount of constraint violation when selecting starting points for the optimization. The sum of squares of the constraint functions must be smaller than cvmargin. Defaults to 10.
- maxcv (float, optional) – Maximal value of the constraint violation (sum of squares of all violated constraint functions) for which the optimization is still considered successful. Defaults to 1e-4.
- solver (str, optional) –
Identifies the optimization algorithm to use. Currently supported values are:
- 'cobyla':
- Uses scipy’s fmin_cobyla function
- 'slsqp':
- Uses scipy’s fmin_slsqp function (default)
- solvercfg (dict, optional) –
Keyword arguments that are passed to the solver. Common options are:
- acc (float)
- Accuracy of the minimization.
- maxiter (int)
- Maximum number of iterations.
- disp (bool)
- Whether to print information about the minimization.
- iprint (int)
- How much information to print.
Defaults to {}.
- par (dict, optional) – Reference values for the model parameters. They are used to determine a metric on observable space (by calling model.getQuadraticForm). For parameters not listed in par the values from model.getDefaultParameters() are used. Defaults to the empty dict.
- obs (dict or None, optional) – Specifies a reference point in observable space. This is only relevant if you want to evolve the population to a homogenous distribution in observable space using evolve. Regions that are far away from obs (depending on the value of temperature) will be avoided. Defaults to None, in which case model.obs is used.
- neighbours (int, optional) – The number of nearest neighbours used to estimate the local point density in observable space. Defaults to 2.
- temperature (float, optional) – Defaults to 1.0. Set this to a larger value to allow evolve to explore a larger volume in observable space.
- penalty (float, optional) – Penalty factor for points that violate the non-linear constraints specified in model. Defaults to 1.0.
- model¶
Model instance
Associated Model instance.
- tries¶
int
Same as tries keyword argument.
- retries¶
int
Same as retries keyword argument.
- cvmargin¶
float
Same as cvmargin keyword argument.
- maxcv¶
float
Same as maxcv keyword argument.
- solver¶
str
Same as solver keyword argument.
- solvercfg¶
dict
Same as solvercfg keyword argument.
- obs¶
dict
Same as obs keyword argument.
- neighbours¶
int
Same as neighbours keyword argument.
- temperature¶
float
Same as temperature keyword argument.
- penalty¶
float
Same as penalty keyword argument.
- __iter__()¶
Return an iterator over the stored points.
Yields: - par (dict) – Model parameters
- obs (dict) – Observables
- chisq (float) – chi-square value
- cons (float) – Constraint violation.
- clear()¶
Clear the data collected with sample or evolve.
- distance(x, y)¶
Compute distance between two points in observable space.
Returns: (float): Distance between x and y.
- evolve(grow, repeat=1, shrink=None, candidates=10, adapt=1.0)¶
Evolve current population towards a more homogenous distribution in observable space.
Parameters: - grow (int) – Number of points to add to the population.
- repeat (int, optional) – Setting repeat to n is equivalent to calling evolve n times with the same arguments (and repeat=1). Defaults to 1.
- shrink (int or None, optional) – Number of points to remove from the population. Defaults to None, in which case grow points are removed.
- candidates (int, optional) – Number of extra candidates to consider for reproduction. Defaults to 10.
- adapt (float, optional) – Level of adaptation. Large values mean faster adaptation. A value of 0 means no adaptation. Defaults to 1.
- find(x)¶
Iterate over collected points, starting with points nearest to x.
Parameters: x (dict) – A point in observable space.
Yields: - p (dict) – Parameter values
- x (dict) – Observable values
- chisq (float) – Chi-square value
- cons (float) – Sum of squared constraint functions.
- fit(obs=None, start=[], tries=None, retries=None, cvmargin=None, maxcv=None, solver=None, solvercfg=None, **kwargs)¶
Find the global minimum of a model’s chi-square function.
Parameters: - obs (dict or None, optional) – Holds the measured values of the observables. Defaults to None, in which case self.model.obs is used.
- start (list of dicts, optional) – Extra starting points to try.
- tries (int or None, optional) – The number of local minimizations to try. Defaults to None, in which case the the value of Fitter.tries is used.
- retries (int or None, optional) – Maximum number of retries (with a different starting point) after a failed minimization. Defaults to None, in which case the value of Fitter.retries is used.
- cvmargin (float or None, optional) – The acceptable amount of constraint violation when selecting starting points for the optimization. The sum of squares of the constraint functions must be smaller than cvmargin. Defaults to None, in which case the value of Fitter.cvmargin is used.
- maxcv (float or None, optional) – Maximal value of the constraint violation (sum of squares of all violated constraint functions) for which the optimization is still considered successful. Defaults to None, in which case the value of Fitter.maxcv is used.
- solver (str or None, optional) –
Identifies the optimization algorithm
to use. Currently supported values are:
- 'cobyla':
- Uses scipy’s fmin_cobyla function
- 'slsqp':
- Uses scipy’s fmin_slsqp function
Defaults to None, in which case the value of Fitter.solver is used.
- solvercfg (dict, optional) –
Keyword arguments that are passed to the solver. Common options are:
acc (float): Accuracy of the minimization. maxiter (int): Maximum number of iterations. disp (bool): Whether to print information about the minimization. iprint (int): How much information to print.Defaults to None, in which case the value of Fitter.solvercfg is used.
- **kwargs (optional) – All other keyword arguments are passed to the fit function, which does the local optimization.
Returns: A FitResult instance with the result of the successful local minimization that found the smallest chi-square.
- nearest(x)¶
Find nearest neighbour to a point in observable space.
Parameters: x (dict) – Point in observable space. - Returns (dict):
- Location of a point p in parameter space which is nearest to x in observable space.
- nnearest(x, n)¶
Find n nearest neighbours to a point in observable space.
Parameters: - x (dict) – Point in observable space.
- n (int) – Number of points to find.
- Returns (list of dict):
- List of dictionaries which specify the locations of (at most) n points p in parameter space which are closest to x in observable space.
- obsiter()¶
Return an iterator over the stored points in observable space.
- pariter()¶
Return an iterator over the stored points in parameter space.
- sample(n, generator=None)¶
Sample the model’s parameter space.
Parameters: - n (int) – Number of points to sample
- generator (callable or None, optional) – Function without arguments which generates a random point in parameter space. Defaults to None, in which case model.generateParameterPoint is used.
- update(par={})¶
Update information about the sample points.
Note
Call this after changing the obs, neighbours, temperature or penalty attributes or after changing the associated Model object.
Parameters: par (dict, optional) – Reference values for the model parameters. They are used to determine a metric on observable space (by calling model.getQuadraticForm). For observables not listed in par the values from model.getDefaultParameters() are used. Defaults to the empty dict.
- myFitter.fit(model, obs=None, start=None, tries=None, basis=None, maxcv=0.0001, autoscale=False, epsilon=1e-08, maxcond=1000000.0, solver='slsqp', raiseFitError=True, solvercfg={})¶
Do a local minimization of a model’s chi-square function.
Parameters: - model (Model instance) – The model to be fitted.
- obs (dict or None, optional) – Dictionary with the ‘measured’ values of the observables. All keys returned by model.getObservableNames() should be present in obs. Defaults to None, in which case model.obs is used.
- start (dict or list of dicts or None, optional) – Starting values of the parameters. If start is a list or tuple of dicts the points in the list are tried in sequence until tries minimizations have been successful. The result of the successful minimization with the smallest chi-square is returned. Defaults to None, in which case model.getDefaultParameters() is used.
- tries (int or None, optional) – The number of successful minimizations to collect before aborting the iteration over the provided starting points. Defaults to None, in which case all provided starting points are tried.
- basis (list of dicts or None, optional) – This argument specifies a linear transformation in parameter space. The list must have as many entries as there are free parameters in the fit. Each dict specifies a vector in parameter space which is used as a basis vector. Defaults to None, in which case the basis is constructed from the scale attributes of the model parameters.
- maxcv (float, optional) – maximal value of the constraint violation (sum of squares of all violated constraint functions) for which the optimization is still considered successful. Defaults to 1e-4.
- autoscale (bool, optional) – If True, a basis for the optimization is constructed from the gradients of the observables. If False, the basis is constructed from the scale attributes of the model parameters. Defaults to False.
- epsilon (float, optional) – Small number used to estimate the derivatives of observables with respect to parameters. This is needed for constructing a basis in parameter space. Irrelevant if autoscale=False. Defaults to 1e-8.
- maxcond (float, optional) – Used for re-scaling the optimization problem. The ratio of the length of the longest basis vector over the length of the shortest basis vector can at most be sqrt(maxcond). Defaults to 1e6. Irrelevant if autoscale=False.
- solver (str, optional) –
Identifies the optimization algorithm to use. Currently supported values are:
- 'cobyla':
- Uses scipy’s fmin_cobyla function
- 'slsqp':
- Uses scipy’s fmin_slsqp function (default)
- raiseFitError (bool, optional) – Whether or not to raise a FitError exception when the model raises a ParameterError exception. Defaults to True.
- solvercfg (dict, optional) –
Keyword arguments that are passed to the solver. Common options are:
- acc (float)
- Accuracy of the minimization.
- maxiter (int)
- Maximum number of iterations.
- disp (bool)
- Whether to print information about the minimization.
- iprint (int)
- How much information to print.
Defaults to {}.
Returns: An instance of FitResult with the results of the fit.
Conversions for p, Z, and chi-square values¶
- myFitter.pvalueFromChisq(chisq, ndof)¶
Computes the p-value from the chi-square value.
Parameters: - chisq (float) – The chi-square value.
- ndof (int) – The number of degrees of freedom.
Returns: The p-value corresponding to the chi-square value chisq, using Wilks’ theorem with ndof degrees of freedom.
Return type: float
- myFitter.chisqFromPvalue(p, ndof)¶
Computes the chi-square value from the p-value.
Parameters: - p (float) – The p-value.
- ndof (int) – The number of degrees of freedom.
Returns: The chi-square value corresponding to the p-value p, using Wilks’ theorem with ndof degrees of freedom.
Return type: float
- myFitter.zvalueFromPvalue(p)¶
Computes the Z-value from the p-value.
Note
The Z-value is often referred to as the ‘number of standard deviations’ or ‘number of sigmas’. myFitter uses two-sided Z-values which are related to the p-value by p = 1 - Erf(Z/sqrt(2))
Parameters: p (float) – The p-value. Returns: The Z-value corresponding to the p-value p. Return type: float
- myFitter.pvalueFromZvalue(z)¶
Computes the p-value from the Z-value.
Note
The Z-value is often referred to as the ‘number of standard deviations’ or ‘number of sigmas’. myFitter uses two-sided Z-values which are related to the p-value by p = 1 - Erf(Z/sqrt(2))
Parameters: z (float) – The Z-value. Returns: The p-value corresponding to the Z-value z. Return type: float
- myFitter.zvalueFromChisq(chisq, ndof)¶
Computes the Z-value from the chi-square value.
Note
The Z-value is often referred to as the ‘number of standard deviations’ or ‘number of sigmas’. myFitter uses two-sided Z-values which are related to the p-value by p = 1 - Erf(Z/sqrt(2))
Parameters: - chisq (float) – The chi-square value.
- ndof (int) – The number of degrees of freedom.
Returns: The Z-value corresponding to the chi-square value chisq, using Wilks’ theorem with ndof degrees of freedom.
Return type: float
- myFitter.chisqFromZvalue(z, ndof)¶
Computes the chi-square value from the Z-value.
Note
The Z-value is often referred to as the ‘number of standard deviations’ or ‘number of sigmas’. myFitter uses two-sided Z-values which are related to the p-value by p = 1 - Erf(Z/sqrt(2))
Parameters: - z (float) – The Z-value.
- ndof (int) – The number of degrees of freedom.
Returns: The chi-square value corresponding to the Z-value z, using Wilks’ theorem with ndof degrees of freedom.
Return type: float
Profilers¶
- class myFitter.Profiler1D(xvar, fitter=None, model=None, xscale=1.0, nsamples=100, tries=5, log=None, useneighbors=True, parallel=None)¶
Compute the profile likelihood on a one-dimensional space.
Note
When the profile likelihood function is to be computed on a 1D grid the stability of the optimisations can be significantly improved by using the best-fit parameters of neighbouring grid points as starting points for local optimisations. The Profiler1D and Profiler2D classes implement this method for one and two-dimensional scans.
For difficult optimisation problems you may need rather detailed control over the procedure for finding the global minima. In this case you can derive a class from Profiler1D and override the fit() method.
The variable in which the profile likelihood is computed can be an arbitrary dependent quantity (not necessarily a model parameter). For a dependent quantity which is not a model parameter a constraint is (temporarily) added to the model. The name of this constraint is '__xscan__'. You should therefore avoid using this name for your own constraints.
Parameters: - xvar (str) – Name of the variable on the x-axis. It must be the name of a dependent quantity in the model (not necessarily a parameter).
- fitter (Fitter or None, optional) – The Fitter object to use for global minimisations. The model whose likelihood is profiled will be fitter.model. Defaults to None, in which case the model argument must be given.
- model (Model or None, optional) – The model whose likelihood function shall be profiled. By specifying the model keyword instead of fitter you disable global optimisations by Fitter objects. Use this only if local optimisations reliably find the global minimum (e.g. because your likelihood function is convex). Defaults to None, in which case fitter must be specified.
- xscale (float, optional) – Scale for the constraint associated with the scan variable. (See Constraint for details.) This argument is irrelevant if the scan variable is a model parameter. nsamples (int, optional): Number of sample points to generate for each global optimisation. Defaults to 100.
- nsamples (int, optional) – Number of points to sample for each global minimisation. Defaults to 100.
- tries (int, optional) – Number of local minimisations to try for finding the global minimum. Defaults to 5.
- log (output stream or None, optional) – Output stream for log messages. Defaults to None, in which case no messages are written.
- useneighbors (bool, optional) – Whether to use best-fit parameters of neighbouring cells as starting points. Defaults to True.
- parallel (dict or None, optional) – Parallelisation options for scans. The dict should hold valid keyword arguments for ParallelFunction. Defaults to None, in which case the scans are not parallelised. Note that using parallelisation effectively sets useneighbors to False.
- fit(xval=None, start=[], sample=True, nsamples=100, tries=5, log=None, **kwargs)¶
Minimise the chi-square for a single grid point.
Note
Derived classes can override this function to implement specific methods for global optimisation. The function should fix the scan variable to xval (using fix()), do local optimisations with all the starting points listed in start, and perform an additional global optimisation if and only if sample is True. The default behaviour is to randomly sample a number of points set by the nsamples attribute and then try a number of local optimisations set by tries.
Parameters: - xval (float) – Value of the scan variable.
- start (list of dicts, optional) – Starting points for local optimisations. The dictionaries will hold values for the model parameters. Defaults to [].
- sample (bool, optional) – Indicates if an additional global optimisation (i.e. random sampling followed by several local optimisations) is required. Defaults to True.
- nsamples (int, optional) – Number of points to sample for each global minimisation. Defaults to 100.
- tries (int, optional) – Number of local minimisations to try for finding the global minimum. Defaults to 5.
- log (output stream or None, optional) – Output stream for log messages. Defaults to None, in which case no messages are written.
- **kwargs (optional) – additional keyword arguments. The default implementation passes them to the myFitter.Fitter.fit() method.
- fix(x)¶
Fix the variable of the profile likelihood.
Note
If the variable of the profile likelihood is a model parameter it is fixed with myFitter.Model.fix(). Otherwise the bound member of the corresponding constraint is adjusted. You will typically use this function in a derived class when you override the fit() method.
Parameters: x (float) – Values of the variables.
- scan(hist, **kwargs)¶
Compute the profile likelihood on a specified grid.
Parameters: - hist (Histogram1D) – A 1D histogram whose xvals member specifies the grid on which the profile likelihood is to be computed. After a successful scan the data values of hist will be FitResult objects holding information about the fit which yielded the smallest chi-square value.
- nsamples (int, optional) – Number of points to sample for each global minimisation. Default value set by constructor.
- tries (int, optional) – Number of local minimisations to try for finding the global minimum. Defaults value set by constructor.
- log (output stream or None, optional) – Output stream for log messages. If None no messages are written. Default value set in constructor.
- useneighbors (bool or None, optional) – Whether to use best-fit parameters of neighbouring cells as starting points. Default value is set in constructor.
- parallel (dict or None, optional) – Parallelisation options for scans. The dict should hold valid keyword arguments for ParallelFunction. Default value is set in the constructor. Note that using parallelisation effectively sets useneighbors to False.
- **kwargs (optional) – Any additional keyword arguments are passed to the fit() method.
- class myFitter.Profiler2D(xvar, yvar, fitter=None, model=None, xscale=1.0, yscale=1.0, nsamples=100, tries=5, log=None, useneighbors=True, parallel=None)¶
Compute the profile likelihood on a two-dimensional space.
Note
When the profile likelihood function is to be computed on a 2D grid the stability of the optimisations can be significantly improved by using the best-fit parameters of neighbouring grid points as starting points for local optimisations. The Profiler1D and Profiler2D classes implement this method for one and two-dimensional scans.
For difficult optimisation problems you may need rather detailed control over the procedure for finding the global minima. In this case you can derive a class from Profile2D and override the fit() method.
The two variables in which the profile likelihood is computed can be arbitrary dependent quantities (not only model parameters). For dependent quantities which are not model parameters a constraint is (temporarily) added to the model. The names of these constraints are '__xscan__' and '__yscan__'. You should therefore avoid using these names for your own constraints.
Parameters: - xvar (str) – Name of the variable on the x-axis. Must be the name of a dependent quantitiy in the model (not necessarily a parameter).
- yvar (str) – Name of the variable on the y-axis. Must be the name of a dependent quantitiy in the model (not necessarily a parameter).
- fitter (Fitter or None, optional) – The Fitter object to use for global minimisations. The model whose likelihood is profiled will be fitter.model. Defaults to None, in which case the model argument must be given.
- model (Model or None, optional) – The model whose likelihood function shall be profiled. By specifying the model keyword instead of fitter you disable global optimisations by Fitter objects. Use this only if local optimisations reliably find the global minimum (e.g. because your likelihood function is convex). Defaults to None, in which case fitter must be specified.
- xscale (float, optional) – Scale for the constraint associated with the variable on the x-axis. (See Constraint for details.) This argument is irrelevant if the corresponding variable is a model parameter.
- yscale (float, optional) – Scale for the constraint associated with the variable on the y-axis. (See Constraint for details.) This argument is irrelevant if the corresponding variable is a model parameter.
- nsamples (int, optional) – Number of points to sample for each global minimisation. Defaults to 100.
- tries (int, optional) – Number of local minimisations to try for finding the global minimum. Defaults to 5.
- log (output stream or None, optional) – Output stream for log messages. Defaults to None, in which case no messages are written.
- useneighbors (bool, optional) – Whether to use best-fit parameters of neighbouring cells as starting points. Defaults to True.
- parallel (dict or None, optional) – Parallelisation options for scans. The dict should hold valid keyword arguments for ParallelFunction. Defaults to None, in which case the scans are not parallelised. Note that using parallelisation effectively sets useneighbors to False.
- fit(xval=None, yval=None, start=[], sample=True, nsamples=100, tries=5, log=None, **kwargs)¶
Minimise the chi-square for a single grid point.
Note
Derived classes can override this function to implement specific methods for global optimisation. The function should fix the scan variables to xval and yval, respectively (using fix()), do local optimisations with all the starting points listed in start, and perform an additional global optimisation if and only if sample is True. The default behaviour is to randomly sample a number of points set by the nsamples attribute and then try a number of local optimisations set by tries.
Parameters: - start (list of dicts, optional) – Starting points for local optimisations. The dictionaries will hold values for the model parameters. Defaults to [].
- sample (bool, optional) – Indicates if an additional global optimisation (i.e. random sampling followed by several local optimisations) is required. Defaults to True.
- nsamples (int, optional) – Number of points to sample for each global minimisation. Defaults to 100.
- tries (int, optional) – Number of local minimisations to try for finding the global minimum. Defaults to 5.
- log (output stream or None, optional) – Output stream for log messages. Defaults to None, in which case no messages are written.
- **kwargs (optional) – additional keyword arguments. The default implementation passes them to the myFitter.Fitter.fit() method.
- fix(x, y)¶
Fix the variables of the profile likelihood.
Note
If the variables of the profile likelihood are model parameters they are fixed with myFitter.Model.fix(). Otherwise the bound members of the corresponding constraints are adjusted. You will typically use this function in a derived class when you override the myFitter.Profiler2D.fit() method.
- scan(hist, **kwargs)¶
Compute the profile likelihood on a specified grid.
Parameters: - hist (Histogram2D) – A 2D histogram whose xvals and yvals members specify the grid on which the profile likelihood is to be computed. After a successful scan the data values of hist will be FitResult objects holding information about the fit which yielded the smallest chi-square value.
- nsamples (int, optional) – Number of points to sample for each global minimisation. Default value set by constructor.
- tries (int, optional) – Number of local minimisations to try for finding the global minimum. Defaults value set by constructor.
- log (output stream or None, optional) – Output stream for log messages. If None no messages are written. Default value set in constructor.
- useneighbors (bool or None, optional) – Whether to use best-fit parameters of neighbouring cells as starting points. Default value is set in constructor.
- parallel (dict or None, optional) – Parallelisation options for scans. The dict should hold valid keyword arguments for ParallelFunction. Default value is set in the constructor. Note that using parallelisation effectively sets useneighbors to False.
- **kwargs (optional) – Any additional keyword arguments are passed to the fit() method.
Gaussian variates¶
- class myFitter.GVar(m, sdev=None)¶
Represents a gaussian random variate with a mean and standard deviation.
Parameters: - m (float or any object with mean and sdev attributes) – If m is a float it specifies the mean of the gaussian variate. Otherwise the mean member of m is taken to be the mean.
- sdev (float or None, optional) – The standard deviation of the gaussian variate. If None the standard deviation is taken from m.sdev (if m has that attribute) or set to zero. Defaults to None.
- mean¶
float
mean of the gaussian variate.
- sdev¶
float
standard deviation of the gaussian variate.
Note
GVar objects support addition, subtraction, multiplication and division with floats or other GVar objects. In the latter case errors are combined in quadrature.
Histograms¶
- class myFitter.Histogram1D(xvals=None, xbins=None, data=None, like=None)¶
Represents one-dimensional histograms.
Parameters: - xvals (list or None, optional) – list of central x-values of the histogram bins. Derived from xbins if None. Defaults to None.
- xbins (list or None, optional) – list of bin boundaries in x direction. Derived from xvals if None. Defaults to None.
- data (array of objects or None, optional) – data members (z-values) of the histogram. If set to None a suitably dimensioned array of None values is created. Defaults to None.
- like (Histogram1D or None, optional) – If not None the central values and bin boundaries of another Histogram1D instance are used. This supercedes any values specified for xvals or xbins. The data member is not copied.
- xvals¶
numpy array
list of central x-values of the histogram bins.
- xbins¶
numpy array
list of bin boundaries in x direction.
- data¶
numpy array
data members (z-values) of the histogram.
Note
Histogram1D supports element-wise addition, subtraction, multiplication, and division with other Histogram1D instances as long as their xvals, yvals, xbins and ybins members are exactly equal. Addition, subtraction, multiplication or division by a constant value for bins is also supported.
- __getitem__(x)¶
Return the data value of a specific bin
Parameters: x (float) – An x coordinate. Returns: The data value of the bin which contains the coordinate x. Raises: KeyError – The coordinate x is outside the range of the histogram.
- __iter__()¶
Iterate over the bin centres.
Yields: x (float) – The x-coordinate of the bin centre.
- __setitem__(x, val)¶
Set the data value of a specific bin
Parameters: - x (tuple) – An x coordinate.
- val – A data value. The value of the bin containing the coordinate x will be set to val.
Raises: KeyError – The coordinate x is outside the range of the histogram.
- center(x)¶
Return the center of the bin to which x belongs.
- copy()¶
Return an independent copy of self.
- errorbars(*args, **kwargs)¶
Plot errorbars with matplotlib.
Parameters: - *args – all positional arguments are passed to matplotlib.axes.Axes.errorbars
- axes (matplotlib.axes.Axes or None, optional) – Axes object to plot to. Uses matplotlib.pyplot.gca() if None. Defaults to None.
- convert (callable or None, optional) – function that converts the elements of self.data to GVar objects. If None, the elements of self.data must be be convertible by the GVar constructor.
- **kwargs – all other keyword arguments are passed to matplotlib.axes.Axes.errorbars.
- iteritems()¶
Iterate over all elements of the histogram.
Yields: tuple – (x, v) where x is the bin center and v the value associated with that bin.
- lb(x)¶
Return the lower bound of the bin to which x belongs.
- max()¶
Return the largest data member in the histogram.
Note
None values are ignored.
- min()¶
Return the smalles data member in the histogram.
Note
None values are ignored.
- plot(*args, **kwargs)¶
Plot the histogram with matplotlib.
Parameters: - *args – all positional arguments are passed to matplotlib.axes.Axes.plot
- axes (matplotlib.axes.Axes or None, optional) – Axes object to plot to. Uses matplotlib.pyplot.gca() if None. Defaults to None.
- convert (callable or None, optional) – function that converts the elements of self.data to floats. If None, the elements of self.data must be floats or have the attribute mean.
- **kwargs – all other keyword arguments are passed to matplotlib.axes.Axes.plot.
- set(h)¶
Set all data values of the histogram.
Parameters: h (Histogram1D or object) – If h is a Histogram1D instance the function iterates over all bins of h and sets the corresponding bins of self to their values. Otherwise all bin values of self are set to h.
- settomax(h)¶
Set all bins to the maximum of their current value and h.
Parameters: h (Histogram1D or object) – If h is a Histogram1D instance the function iterates over all bins of h and sets the corresponding bins of self to the maximum of the two values. Otherwise all bins of self are set to the maximum of their current value and h.
- settomin(h)¶
Set all bins to the minimum of their current value and h.
Parameters: h (Histogram1D or object) – If h is a Histogram1D instance the function iterates over all bins of h and sets the corresponding bins of self to the minimum of the two values. Otherwise all bins of self are set to the minimum of their current value and h.
- setxlim(axes=None)¶
Set x limits of the current plot.
Parameters: axes (matplotlib.axes.Axes or None) – Axes object whose limits are to be set. Uses matplotlib.pyplot.gca() if None. Defaults to None.
- ub(x)¶
Return the upper bound of the bin to which x belongs.
- class myFitter.Histogram2D(xvals=None, yvals=None, xbins=None, ybins=None, data=None, like=None)¶
Represents two-dimensional histograms.
Parameters: - xvals (list or None, optional) – list of central x-values of the histogram bins. Derived from xbins if None`. Defaults to ``None.
- yvals (list or None, optional) – list of central y-values of the histogram bins. Derived from ybins if None. Defaults to None.
- xbins (list or None, optional) – list of bin boundaries in x direction. Derived from xvals if None. Defaults to None.
- ybins (list or None, optional) – list of bin boundaries in y direction. Derived from yvals if None. Defaults to None.
- data (2D array of objects or None, optional) – data members (z-values) of the histogram. The first index corresponds to the y-axis. If set to None a suitably dimensioned array of None values is created. Defaults to None.
- like (Histogram2D or None, optional) – If not None the central values and bin boundaries of another Histogram2D instance are used. This supercedes any values specified for xvals, yvals, xbins, or ybins. The data member is not copied. Defaults to None.
- xvals¶
numpy array
list of central x-values of the histogram bins.
- yvals¶
numpy array
list of central y-values of the histogram bins.
- xbins¶
numpy array
list of bin boundaries in x direction.
- ybins¶
numpy array
list of bin boundaries in y direction.
- data¶
numpy array
data members (z-values) of the histogram. The first index corresponds to the x-axis.
Note
Histogram2D supports element-wise addition, subtraction, multiplication, and division with other Histogram2D instances as long as their xvals, yvals, xbins and ybins members are exactly equal. Addition, subtraction, multiplication or division by a constant value for bins is also supported.
- __getitem__(xy)¶
Return the data value of a specific bin
Parameters: xy (tuple) – A pair of coordinates. Returns: The data value of the bin which contains the coordinates xy. Raises: KeyError – The coordinates xy are outside the range of the histogram.
- __iter__()¶
Iterate over the bin centres.
Yields: - x (float) – The x-coordinate of the bin centre.
- y (float) – The y-coordinate of the bin centre.
- __setitem__(xy, val)¶
Set the data value of a specific bin
Parameters: - xy (tuple) – A pair of coordinates.
- val – A data value. The value of the bin containing the coordinates xy will be set to val.
Raises: KeyError – The coordinates xy are outside the range of the histogram.
- center(x, y)¶
Return the center of the bin to which (x,y) belongs.
- contour(axes=None, convert=None, **kwargs)¶
Draw contour lines with matplotlib
Parameters: - axes (matplotlib.axes.Axes or None, optonal) – Axes object to plot to. Uses matplotlib.pyplot.gca() if None. Defaults to None.
- convert (callable or None, optional) – function that converts the elements of self.data to floats. If None, the elements of self.data must be floats. Defaults to None.
- **kwargs – all other keyword arguments are passed to matplotlib.axes.contour.
- contourf(axes=None, convert=None, **kwargs)¶
Draw filled contours with matplotlib
Parameters: - axes (matplotlib.axes.Axes or None, optional) – Axes object to plot to. Uses matplotlib.pyplot.gca() if None. Defaults to None.
- convert (callable or None, optional) – function that converts the elements of self.data to floats. If None, the elements of self.data must be floats. Defaults to None.
- **kwargs – all other keyword arguments are passed to matplotlib.axes.contourf.
- copy()¶
Return an independent copy of self.
- iteritems()¶
Iterate over all elements of the histogram.
Yields: tuple – ((x, y), v) where (x, y) is the bin center and v the value associated with that bin.
- lb(x, y)¶
Return the lower left corner of the bin to which (x,y) belongs.
- max()¶
Return the largest data member in the histogram.
Note
None values are ignored.
- min()¶
Return the smallst data member in the histogram.
Note
None values are ignored.
- pcolormesh(axes=None, convert=None, **kwargs)¶
Draw a colored mesh with matplotlib
Parameters: - axes (matplotlib.axes.Axes or None, optional) – Axes object to plot to. Uses matplotlib.pyplot.gca() if None. Defaults to None.
- convert (callable or None, optional) – function that converts the elements of self.data to floats. If None, the elements of self.data must be floats. Defaults to None.
- **kwargs – all other keyword arguments are passed to matplotlib.axes.pcolormesh.
- set(h)¶
Set all data values of the histogram.
Parameters: h (Histogram2D or object) – If h is a Histogram2D instance the function iterates over all bins of h and sets the corresponding bins of self to their values. Otherwise all bin values of self are set to h.
- settomax(h)¶
Set all bins to the maximum of their current value and h.
Parameters: h (Histogram2D or object) – If h is a Histogram2D instance the function iterates over all bins of h and sets the corresponding bins of self to the maximum of the two values. Otherwise all bins of self are set to the maximum of their current value and h.
- settomin(h)¶
Set all bins to the minimum of their current value and h.
Parameters: h (Histogram2D or object) – If h is a Histogram2D instance the function iterates over all bins of h and sets the corresponding bins of self to the minimum of the two values. Otherwise all bins of self are set to the minimum of their current value and h.
- ub(x, y)¶
Return the upper right corner of the bin to which (x,y) belongs.
- myFitter.cumulatedHistogram(h, upper=False, const=None)¶
Compute the cumulated distribution.
Parameters: - h (Histogram1D) – the histogram to cumulate
- upper (bool, optional) – If True, the histogram is cumulated from the upper end. Defaults to False.
- const (optional) – Constant to be added to all bins of the resulting histogram. Defaults to None, in which case nothing is added.
Returns: The cumulated histogram.
Return type: Histogram1D
Note
If hc = cumulated(h, upper=False, const=c) then hc.data[i] = sum(h.data[:i+1]) + c for all i in range(len(h.data)). If hc = cumulated(h, upper=True, const=c) then hc.data[i] = sum(h.data[i:]) + c for all i in range(len(h.data)).
- myFitter.densityHistogram(h)¶
Divide all bin values by the bin width (Histogram1D) or bin area (Histogram2D).
Parameters: h (Histogram1D or Histogram2D) – the histogram to convert. h is not modified. Returns: Histogram1D or Histogram2D: the converted histogram.
Integration and toy simulations¶
- class myFitter.IntegrationResult(itnres=[])¶
Summarizes the results of a vegas integration.
Parameters: itnres (list of GVar, optional) – list of GVar objects (or anything that has attributes ‘mean’ and ‘sdev’) corresponding to the results of individual iterations. Defaults to an empty list. - mean¶
mean value of weighted average
- sdev¶
standard deviation of weighted average
- chisq¶
chi-square value of the results of individual iterations
- itnres¶
same as itnres keyword argument.
Note
You can join several IntegrationResult instances by adding them. Here is an example which updates and IntegrationResult result after each iteration and prints information about the current state of the integration:
f = ... integ = Integrator(...) results = IntegrationResult() print results.hdr() for i in range(10): results += integ(f, nitn=1, neval=500) print results.info()
- copy()¶
Return an independent copy.
- drop(n)¶
Remove the results of the first n iterations.
Parameters: n (int) – number of iterations to remove.
- hdr()¶
Return the header for a running summary of the integration as a string.
- info()¶
Return information about the last iteration and the current average as a string.
Note
Use together with hdr().
- myFitter.integrationResults(n)¶
Return an array of empty IntegrationResult instances.
Parameters: n – number of elements of the array.
- class myFitter.Integrator(domain, **kwargs)¶
Simple wrapper around vegas.Integrator.
Parameters: - domain (list) – Integration domain. Each element of the list should be a list or tuple with two elements defining the lower and upper bound of the integration domain of the related variable.
- parallel (dict or None, optional) – Parallelisation options. The dict should hold valid keyword arguments for ParallelFunction. Defaults to None, in which case the integrand is not parallelised.
- drop (int, optional) – Number of initial iterations to exclude from the weighted average. Defaults to 0.
- log (output stream or None, optional) – Output stream for log messages. Defaults to None, in which case no log messages are printed.
- **kwargs (optional) – All other keyword arguments are passed down to the vegas.Integrator constructor.
- __call__(f, **kwargs)¶
Carries out the integration.
Parameters: - f (callable) – The integrand.
- **kwargs (optional) – Additional keyword arguments are the same as in the constructor and override the values specified there. For the parallel keyword the dicts are merged.
Returns: An object holding the results of the iterations and their weighted average. If the integrand returns a list or array the return value is a numpy array of IntegrationResult objects.
Return type: IntegrationResult
- config(**kwargs)¶
Change or read configuration options.
Note
This is essentially the same as the vegas.Integrator.set() method. The configuration dict contains an additional keywords 'parallel', 'drop', and 'log'.
Parameters: **kwargs (optional) – Configuration options to set. All keywords accepted by vegas.Integator.set() as well as parallel, drop, and log are valid. Returns: The old configuration. Return type: dict
- fill(f, neval, *hist, **kwargs)¶
Fill histograms with data.
Parameters: - f (callable) – function to integrate.
- neval (int) – number of evaluations.
- *hist – tuples describing the histograms to fill.
- **kwargs (optional) – Allowed keyword arguments are the same as for the constructor and can be used to override settings made there.
Note
The function f must be an integrand function. It should take a single numpy array x as argument and return an array whose first element is the function value of the integrand. The other elements can be ‘binned’. The *hist arguments must be of the form (j, h) where h is a Histogram1D or Histogram2D instance and j can be a callable object, a tuple of integers or an integer.
If h is a Histogram1D instance and j is an integer each bin of h with boundaries a and b will be filled with a GVar object holding the estimate of the integral of f(x)[0] over the set defined by a <= f(x)[j] < b. Alternatively j can be a tuple of one integer. If j is a callable object and h a Histogram1D instance the integration domain for each bin is defined by a <= j(x, f(x)) < b.
If h is a Histogram2D instance and j is a tuple of two integers each bin of h with x-boundaries ax and bx and y-boundaries ay and by will contain an estimate of the integral of f(x)[0] over the domain with ax <= f(x)[j[0]] < bx and ay <= f(x)[j[1]] < by. If j is a callable it should return a tuple of two numbers and the integration domain is defined by ax <= j(x, f(x))[0] < bx and ay <= j(x, f(x))[1] < by.
Returns: The value (and error) of the integral. Return type: GVar
- random(neval=None, **kwargs)¶
Generate random points.
Parameters: - neval (int or None, optional) – Maximum number of points yielded by the iterator. Defaults to None, in which case the value of the neval setting is used. Note that the number of yielded points will typically be less than neval (usually about half).
- **kwargs (optional) – All additional keyword arguments are passed down to vegas.Integrator.random.
Yields: - x (numpy array) – A random point in the integration domain.
- w (float) – The weight of the point. The weights of all yielded points add up to 1.
- class myFitter.LRTIntegrand(fitter0, fitter1, dchisq=None, nested=False, verbose=0)¶
Integrand function for computing p-values in LRTs.
Note
Pass instances of LRTIntegrand to myFitter.ToySimulator.__call__() to compute the p-values numerically.
Parameters: - fitter0 (Fitter) – Fitter instance which fits the model representing the null hypothesis of the LRT.
- fitter1 (Fitter) – Fitter instance which fits the model representing the alternative hypothesis of the LRT.
- dchisq (float or None, optional) – Observed value of the Delta chi-square. Defaults to None.
- nested (bool, optional) – Set to True when the models are nested, i.e. when fitter0.model was obtained from fitter1.model by fixing parameters or adding constraints. Defaults to False.
- verbose (int, optional) – Amount of information to print to stdout. Defaults to 0, in which case no information is printed.
- fitter0¶
Fitter
Same as fitter0 argument.
- fitter1¶
Fitter
Same as fitter1 argument.
- dchisq¶
float or None
Same as dchisq argument.
- nested¶
bool
Same as nested argument.
- verbose¶
int
Same as verbose argument.
- nshots¶
int
Number of integrand evaluations (since last call to myFitter.LRTIntegrand.reset()).
- nfail¶
int
Number of failed integrand evaluations (since last call to myFitter.LRTIntegrand.reset()).
- __call__(x)¶
Evaluate the integrand.
Parameters: x (dict) – The point in observable space. Returns: numpy array of 2 floats: The second element is the Delta chi-square value for x. The first element is 0 if this value is smaller than the value of dchisq set in the constructor or if one of the fits failed to find a feasible solution. In all other cases the first element is 1.
- class myFitter.ToySimulator(model0, par0={}, model1=None, par1=None, dchisq=0.0, smart=True, ifrac=0.25, ipow=2.0, minrange=2.5, epsilon=1e-06, tol=1e-06, **kwargs)¶
Class for running toy simulations and computing p-values.
Note
ToySimulator is a subclass of Integrator. It can use a “smart” sampling method which is taylored to p-value computations in (nested or non-nested) LRTs. To do this it requires additional information about the alternative hypothesis and the Delta chi-square. If you do not provide this information ToySimulator uses standard sampling (i.e. generates points distributed according to the PDF associated with your null hypothesis).
Parameters: - model0 (Model) – Model instance which defines the PDF.
- par0 (dict, optional) – Parameter values for the model. Model defaults are used for unspecified parameters. Defaults to {}.
- model1 (Model or None, optional) – Model instance which describes the alternative hypothesis. Only required if you want to use smart sampling. Defaults to None.
- par1 (dict or None, optional) – Parameter values for model1. Model defaults are used for unspecified parameters. Defaults to {}.
- dchisq (float, optional) – Delta chi-square value for the LRT. Only relevant if you want to use smart sampling. Defaults to 0.
- smart (bool, optional) – Whether to use smart sampling. Defaults to True.
- ifrac (float, optional) – Fraction of sample points to put in “inner region”. Only relevant if you use smart sampling. Defaults to 0.25.
- ipow (float, optional) – Power law to use for sampling the “inner region”. Only relevant if you use smart sampling. Defaults to 2.
- minrange (float, optional) – When using smart sampling, parameters which only float in a very small range should be considered as fixed for the purpose of constructing the smart sampling density. If the range of a parameter is smaller than minrange times its scale attribute it is considered as fixed for this purpose. Defaults to 2.5.
- epsilon (float, optional) – Small parameter to compute numerical derivatives. Only relevant if you use smart sampling. Defaults to 1e-6.
- tol (float, optional) – Tolerance to use for orthogonalising vectors. Only relevant if you use smart sampling. Defaults to 1e-6.
- **kwargs (optional) –
Additional keyword arguments are passed down to the constructor of vegas.Integrator. The most important keywords are:
- nitn
- The number of iterations.
- neval
- The number of function evaluations per iteration.
- __call__(g, **kwargs)¶
Integrate a function on observable space.
Parameters: - g (callable) –
The function to integrate. g should take a dict of observable values as argument and may return a float or a one-dimensional numpy array of floats. This computes the integral

where
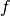 is the PDF of model0 and
is the PDF of model0 and 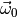 the parameter point par0 (both specified in the constructor).
the parameter point par0 (both specified in the constructor). - **kwargs (optional) –
Additional keyword arguments are passed down to the __call__ method of Integrator. The most important keywords are:
- nitn
- The number of iterations.
- neval
- The number of function evaluations per iteration.
- parallelize
- dict of parallelisation options.
- g (callable) –
- fill(g, neval, *hist, **kwargs)¶
Fill histograms with data.
Parameters: - g (callable) – function to integrate.
- neval (int) – number of evaluations.
- *hist – tuples describing the histograms to fill.
- **kwargs (optional) – Allowed keyword arguments are the same as for the constructor and can be used to override settings made there.
Note
The function f must be function on observable space. It should take a dict x representing the point in observable space as argument and return an array whose first element is the function value of the integrand. The other elements can be ‘binned’. The *hist arguments must be of the form (j, h) where h is a Histogram1D or Histogram2D instance and j can be a callable object, a tuple of integers or an integer.
If h is a Histogram1D instance and j is an integer each bin of h with boundaries a and b will be filled with a GVar object holding the estimate of the integral of f(x)[0] over the set defined by a <= f(x)[j] < b. Alternatively j can be a tuple of one integer. If j is a callable object and h a Histogram1D instance the integration domain for each bin is defined by a <= j(x, f(x)) < b.
If h is a Histogram2D instance and j is a tuple of two integers each bin of h with x-boundaries ax and bx and y-boundaries ay and by will contain an estimate of the integral of f(x)[0] over the domain with ax <= f(x)[j[0]] < bx and ay <= f(x)[j[1]] < by. If j is a callable it should return a tuple of two numbers and the integration domain is defined by ax <= j(x, f(x))[0] < bx and ay <= j(x, f(x))[1] < by.
Returns: The value (and error) of the integral. Return type: GVar
- random(**kwargs)¶
Generate random points in observable space.
Note
This function returns an iterator which generates points in observable space distributed according to a Gaussian approximation of the PDF of model0 with parameters par0 (both set in the constructor). If model0 has only Gaussian observables the approximation is exact.
Parameters: **kwargs (optional) – Keyword arguments to be passed to Integrator.random. The most important one is neval, which defines the maximal number of points yielded by the iterator.
Yields: - obs (dict) – The point in observable space.
- weight (float) – The weight of the point. The iterator yields neval points and their weights sum to 1. For models with only Gaussian observables all weights will be the same.
Parallelisation¶
- class myFitter.ParallelFunction(f, njobs=2, batchsize=None, workdir='.', prefix=None, init=None, runner=<class myFitter.parallelize.LocalRunner at 0x7f74571bba10>, tries=2, log=None, refresh=1, cleanup=2)¶
Class for parallel function evaluation.
Note
ParallelFunction objects are callable and accept a numpy array or list of python objects as argument. They parallelise the task of applying a certain function to each element of the array. Process communication is done via files and the parallel jobs can be run on different nodes of a computing cluster.
Parameters: - f (callable) – Function to parallelise. It should only take a single argument.
- njobs (int, optional) – Number of parallel jobs. Defaults to 2.
- batchsize (int or None) – Number of evaluations done sequentially in each job. If not None this overrides the value of njobs, since the ParallelFunction object will create as many jobs as needed to achieve the desired batch size. Defaults to None.
- workdir (str, optional) – Directory for keeping temporary files (for process communication). Defaults to '.'.
- prefix (str or None) – Prefix to use for temporary files. Defaults to None, in which case a unique file name is generated automatically.
- runner (subclass of BasicRunner, optional) – Class (not instance) which defines the details of the parallelisation. You can choose from the pre-defined classes LocalRunner and SlurmRunner or define your own by deriving from BasicRunner. Defaults to LocalRunner.
- tries (int, optional) – Maximal number of attempts to re-start a crashed job. Defaults to 2.
- log (output stream or None, optional) – Output stream for log messages. Defaults to None, in which case no messages are printed.
- refresh (int, optional) – Time interval (in seconds) in which status of running jobs is checked. Defaults to 1.
- cleanup (int, optional) – Indicates how much of the temporary data will be deleted after all jobs have finished. Defaults to 2 in which case all files except non-empty error logs are removed. If cleanup is 0 no files are removed.
- myFitter.parallel(**kwargs)¶
Decorator for parallelising a function.
Note
Use as follows:
@parallel(...) def myfunc(x): ...
The arguments for parallel are the same as for ParallelFunction, but without the initial argument f. The defined function is parallelised and should only take a single argument.
- class myFitter.BasicRunner(name, batchid, workdir, script, args, stdout, stderr, pyexec='/usr/bin/python')¶
Base class for runners (classes that control individual parallel jobs).
Parameters: - name (str) – The name of the group of parallel jobs.
- batchid (int) – The number of the parallel job.
- workdir (str) – The working directory (for temporary files). The path may be relative.
- script (str) – The name of the python script to run. Includes the path, which may be relative.
- args (list of str) – Command line arguments to pass to the Python script.
- stdout (str) – Name of the file to which STDOUT output of the script should be re-directed. Includes the path, which may be relative.
- stderr (str) – Name of the file to which STDERR output of the script should be re-directed. Includes the path, which may be relative.
- pyexec (str, optional) – Name and path to the Python executable to use. Defaults to sys.executable.
- running¶
bool
True if the job is currently running.
- finished¶
bool
True if the job has finished (normally or abnormally).
- name¶
str
Same as keyword argument name.
- batchid¶
int
Same as keyword argument batchid.
- workdir¶
str
Same as keyword argument workdir.
- script¶
str
Same as keyword argument script.
- args¶
list of str
Same as keyword argument args.
- stdout¶
str
Same as keyword argument stdout.
- stderr¶
str
Same as keyword argument stderr.
- pyexec¶
str
Same as keyword argument pyexec.
- cancel()¶
Cancel the job.
Note
Derived classes must implement this. The job should be cancelled, self.running should be set to False and self.finished to True.
- poll()¶
Update the job status.
Note
Derived classes must implement this. If the job is pending (not started yet) it should set self.running and self.finished to False. If the job is currently running it should set self.running to True and self.finished to False. If the job has finished (normally or abnormally) it should set self.running to False and self.finished to True.
- class myFitter.LocalRunner(*args, **kwargs)¶
Run job as independent process on local machine.
- class myFitter.SlurmRunner(*args, **kwargs)¶
Submit job to the SLURM batch system.