Fitting the model

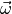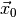The first thing you probably want to do after defining a model is fitting it to the observed data. By “fitting” one usually means computing the maximum likelihood estimates of the model parameters for the observed data (see Statistical inference for details). Thus, we have to find values 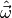for the model parameters which minimise the chi-square function. For smooth chi-square functions there are many efficient algorithms which can find local minima, but finding the global minimum can be rather difficult. myFitter employs a mixed strategy for global optimisation: the parameter space is first explored by random sampling, and then several local optimisations are performed which use the best candidates of the random sample as starting points. There is no guarantee that this method always finds the global minimum, but with a certain amount of tuning it tends to work reliably for most problems.

Global minimisations are done in myFitter with the Fitter class. A Fitter object can sample a model’s parameter space, store the sampled points, and perform local minimisations. For instance, the model from The Model class can be fitted as follows (see also fit_example.py):

model = MyModel()
fitter = Fitter(model)
fitter.sample(100)
globalmin = fitter.fit(tries=5)

In line 1 we create an instance of MyModel, and in line 2 we create a Fitter object for this model. In line 3 we sample the parameter space with 100 points. myFitter tries to guess reasonable distributions for the model parameters from their default, scale and bounds attributes (see Parameter for details). By default the distributions of the parameters are independent. There are three different ways in which you can modify the sampling distribution of your parameters:

1. Set the generator attribute of your model parameters to a function of your choice. The function should take zero arguments and return a random value for the parameter.
2. Override the generateParameterPoint() method of you model class. The method should take zero arguments and return a dictionary with random values for all parameters.
3. Set the generator keyword argument of the sample() method to a function of your choice. The function should take zero arguments and return a dictionary with random values for all parameters.

Note that options 2 and 3 allow you to implement correlations between your parameters. If you call the sample() method a second time more points are added to the sample, but the old points are not deleted. You can use this to sample a specific region in parameter space with a higher density. Simply adjust the bounds or generator attributes of the relevant parameters and sample again. To clear the list of sample points you can use the clear() method.

In line 4 we compute the global minimum of the chi-square function by running 5 local minimisations, using the sample points with the 5 lowest chi-square values as starting points. The return value of Fitter.fit() is an instance of FitResult and stores information about the best solution which was found. The members of FitResult are:

bestFitParameters

A dict holding the parameter values at the minimum.

minChiSquare

The chi-square value at the minimum.

constraintViolation

Sum of the squares of the constraint functions for which the constraint is violated.

feasible

Boolean value indicating if the solution has an acceptably small constraint violation. The acceptable level of constraint violation can be set by the maxcv argument to Fitter.fit() or fit().

success

Boolean value indicating if the minimization terminated successfully.

status

Exit code returned by the minimiser.

message

String holding the message returned by the minimizer.

nEvaluations

Number of function evaluations needed to find the minimum.

myFitter defines a total ordering for FitResult objects in the following way: all feasible solutions are smaller than all unfeasible solutions. If two solutions are feasible their minChiSquare attributes are compared. If two solutions are unfeasible their constraintViolation attributes are compared. You can therefore compare two FitResult objects with the operators <, ==, > etc. just as if they were real numbers. The “best” solution returned by Fitter.fit() is the smallest one which was found with respect to this ordering. The FitResult also defines the __str__() method, so you can obtain a nice and readable summary of the fit result. For the example from The Model class we get:

>>> print globalmin
best-fit parameters:
  obs1 syst = 0.0924404116775
  p1        = 1.20636170236
  p2        = 0.828938775851
minimum chi-square:    -9.62023886287
number of evaluations: 8
constraint violation:  0
Optimization terminated successfully.

The Fitter.fit() method accepts a number of keyword arguments which let you control the details of the optimisation procedure. The most important ones are:

obs

A dictionary holding the measured values of the observables. Use this to override the values stored in model.obs.

tries

The number of local minimisations to try.

start

A list of dicts holding additional starting points for local minimisations. These starting points are tried in addition to the ones specified by tries.

cvmargin

If your model has constraints some of the sample points will inevitably violate these constraints. cvmargin specifies the maximal amount of constraint violation a given sample point can have in order to be selected as starting point for a local minimisation.

maxcv

The maximum amount of constraint violation a solution can have in order to be considered feasible. Defaults to 1e-4

solver

A string which indicates the minimisation algorithm to use. Currently myFitter supports two minimisers from the SciPy package: the COBYLA ('cobyla') algorithm, which is a derivative-free algorithm for constrained optimisation, and the SLSQP ('slsqp') algorithm, which is a gradient search algorithm that can handle non-linear constraints and computes the gradients numerically if necessary. The default setting is 'slsqp', which generally gives the best results for smooth chi-square functions.

solvercfg

A dict holding configuration options for the solver. Allowed keys depend on the solver, but some options are common to all solvers. These options are:

'acc'

Required accuracy of the minimisations. The exact meaning depends on the solver. Defaults to 1e-5.

'maxiter'

Maximum number of iterations. Defaults to 1000.

'disp'

Boolean indicating if information about the minimisation should be printed. Defaults to False.

'iprint'

Integer indicating the amount of information to print. Exact meaning depends on the solver. Defaults to 1.

The same keyword arguments can also be given to the constructor of Fitter. In this case the Fitter object will remember the the specified values and use them as defaults when the fit() method is called. Any keywords passed to fit() directly override the defaults.

The local minimisations are actually done by a function called fit(), which is different from and invoked by the method Fitter.fit(). Any keyword arguments that Fitter.fit() doesn’t recognise are handed down to fit().